In the world of semiconductors, it should come as no surprise to hear about the numerous benefits of using analog in-memory computing, which promises significantly better peak performance and energy efficiency than traditional digital architectures such as GPUs in matrix-vector multiplications. Through this approach, it is possible to minimize data movement and perform the entire multiplication in a single cycle, significantly reducing energy consumption while also offering orders-of-magnitude improvements in speed and computational density compared to digital architectures.
However, the critical factors preventing this approach from being widely adopted in the development of AI accelerators are also well known. Among these factors is the substantial device variability introduced during fabrication, which is not modeled by a software neural network. These device mismatches and non-idealities arise due to imperfections in the fabrication process, inevitably introducing layer-specific errors in gradient computation. With backpropagation through the network, such errors are substantially amplified, resulting in severe degradation of neural network performance. As a result, a memristor crossbar cannot be arbitrarily large, making it impossible to develop scalable solutions using conventional methods.
To make matters worse, the standard solution proposed to address this issue typically involves adding digital-to-analog (DAC) and analog-to-digital (ADC) conversions between network layers. However, this technique comes at the cost of excessively increasing energy consumption, rendering all efforts ineffective. Therefore, it is necessary to completely rethink the approach to analog in-memory computing to make its benefits viable in the real world.
With this in mind, Fractile AI, a UK-founded AI hardware company, is pursuing a radical new approach to training an analog neural network in situ on the hardware, enabling this disruptive technology to become reality.
Equilibrium propagation and nonlinear resistive networks
The AI accelerator proposed by Fractile is based on Equilibrium Propagation, a learning framework for energy-based models that simultaneously solves several practical problems of analog neural networks, providing a complete foundation for in-situ machine learning.




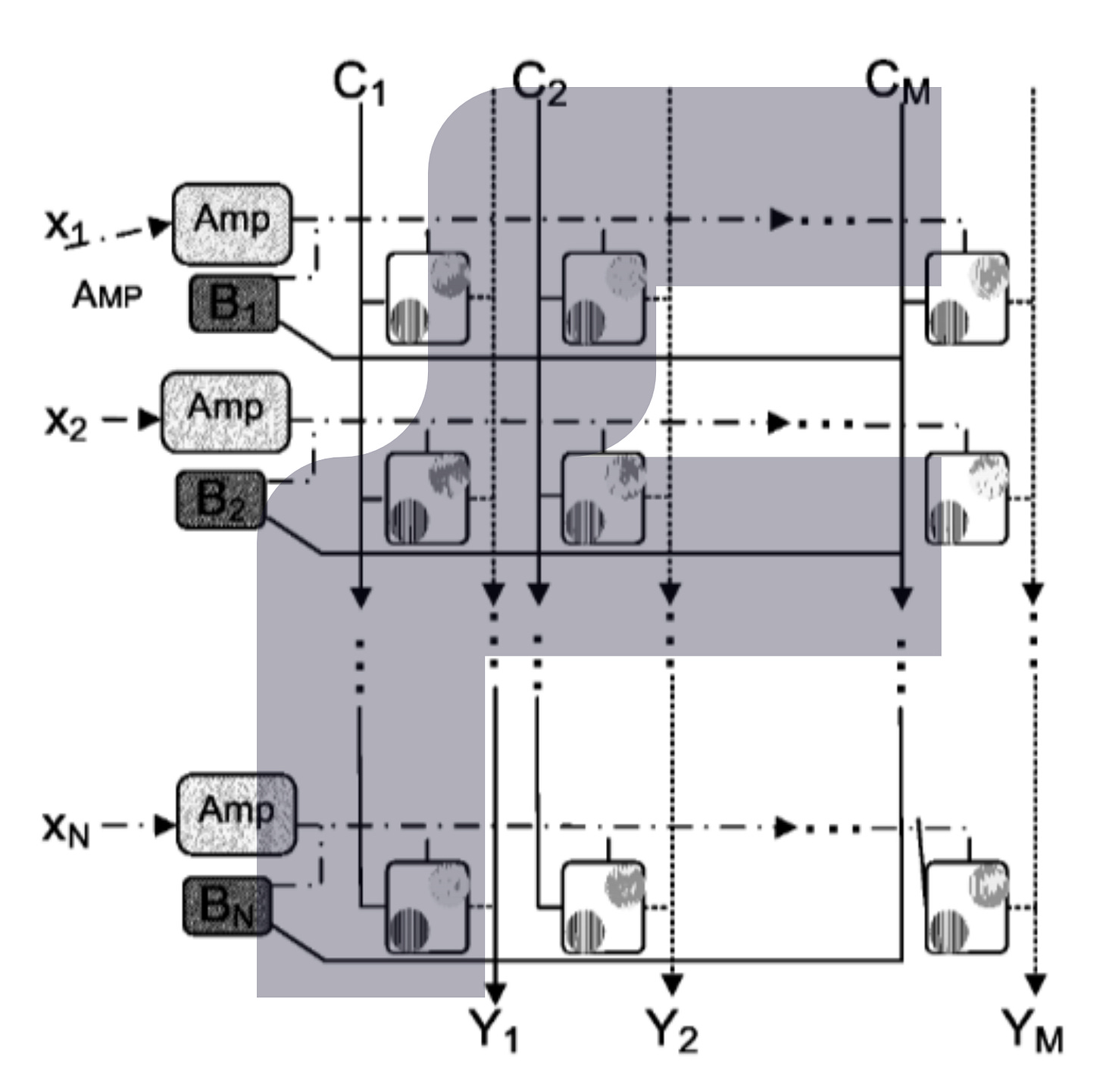
The basic idea behind this accelerator is the use of nonlinear resistive networks based on programmable resistors, such as an NVM crossbar array of RRAM devices, with an energy function that naturally arises as a direct consequence of Kirchhoff’s laws. These networks consist of programmable resistors, whose conductances act as synaptic weights; diodes, which form nonlinear transfer functions; voltage sources, used to define data samples at input nodes; and current sources, used to inject loss gradient signals during training. As a result, such analog networks can be trained via stochastic gradient descent using information locally available for each weight.
In the proposed method, the gradient is computed as an objective function corresponding to local perturbations, performed using leaky integrator neural computation. This process handles both inference in the first phase and backpropagation of error derivatives in the second phase. In this way, the gradient of the loss function to be minimized with respect to a conductance can be estimated solely by measuring the voltage drop across the corresponding resistor. Furthermore, the analog circuit which is responsible for performing multiply and scaling operations has included a feedback connection and the gain of the differential amplifier designed in such a way as to cancel the value of constants which are implementation dependent and therefore cancel the effects of manufacturing and design variation on the output of analog neuron.
By using this method to perform credit assignment directly through hardware physics while implicitly incorporating information about device variability, it enables the development of an end-to-end analog neural network platform. Unlike naive backpropagation, computed updates seamlessly correct for many types of variability and imperfections that are ubiquitous in analog electronic devices. Furthermore, this method completely eliminates the need for embedded ADCs and DACs and enables training and inference with orders of magnitude greater efficiency than a conventional GPU.
The in situ process
The training and inference processes of the proposed accelerator are carried out in distinct stages using the measurement of electrical signals at the output after clipping the input voltages corresponding to the data. In the training process, an electrical signal corresponding to the training data is obtained and clamped to the input of the entire neural network, while the output of the neural network is clamped to an electrical signal representing the ground truth value of the training data.
The electrical signals from the clamped input and clamped output propagate through the analog neural network layers. The electrical signal from the clamped input propagates forward toward the output of the neural network, while the electrical signal from the clamped output propagates backward toward the input of the neural network. Eventually, the propagating signals reach equilibrium within the analog neural network.


At this point, a verification process is performed to determine whether equilibrium has been achieved while the analog neural network is in the double-clamp state. This verification is done after a short waiting period by taking repeated measurements of an electrical signal in the analog neural network and checking whether the measurements remain consistent. Once equilibrium has been achieved in the double-clamp state, a measurement and update process occurs in parallel for each layer of the analog neural network and for each neuron within each layer. During the transition to equilibrium in the double-clamp state, each error element stores information about the change in the electrical signal within the element, which is a resistor. Measurements are then taken from the error element—specifically, in the case of a resistor, by reading the voltage difference. The amount of change in the electrical signal measured from the error elements corresponds to a gradient signal used to train the neural network, with weight updates based on the difference between the neural network’s natural equilibrium output under the first clamp (input) and the target output. By updating the neural network’s weights based on the error element measurements, the network can be trained effectively.
Finally, a check is performed to determine whether convergence has been achieved, such as by verifying whether the update made to the programmable electronic elements falls below a threshold or whether a predetermined number of training examples has been used. If convergence has been reached, training ends. Otherwise, the process repeats for another training cycle.
In turn, the inference process follows a similar approach; however, there is no clamping of the neural network output. As previously described, the input electrical signal is applied to the neural network input, such as by clamping the electrical signal to the input. This input represents a piece of data to be inferred by the network. As a result of the applied input electrical signal, the signal propagates through the analog neural network layers from the input toward the output. At this point, a check is performed to determine whether equilibrium or a stable state has been reached in the neural network. As in the training process, this check may involve waiting for a specified time and assuming that equilibrium has been reached. Once equilibrium is achieved, the electrical signal at the output of the neural network is read and either stored or sent to a subsequent process.

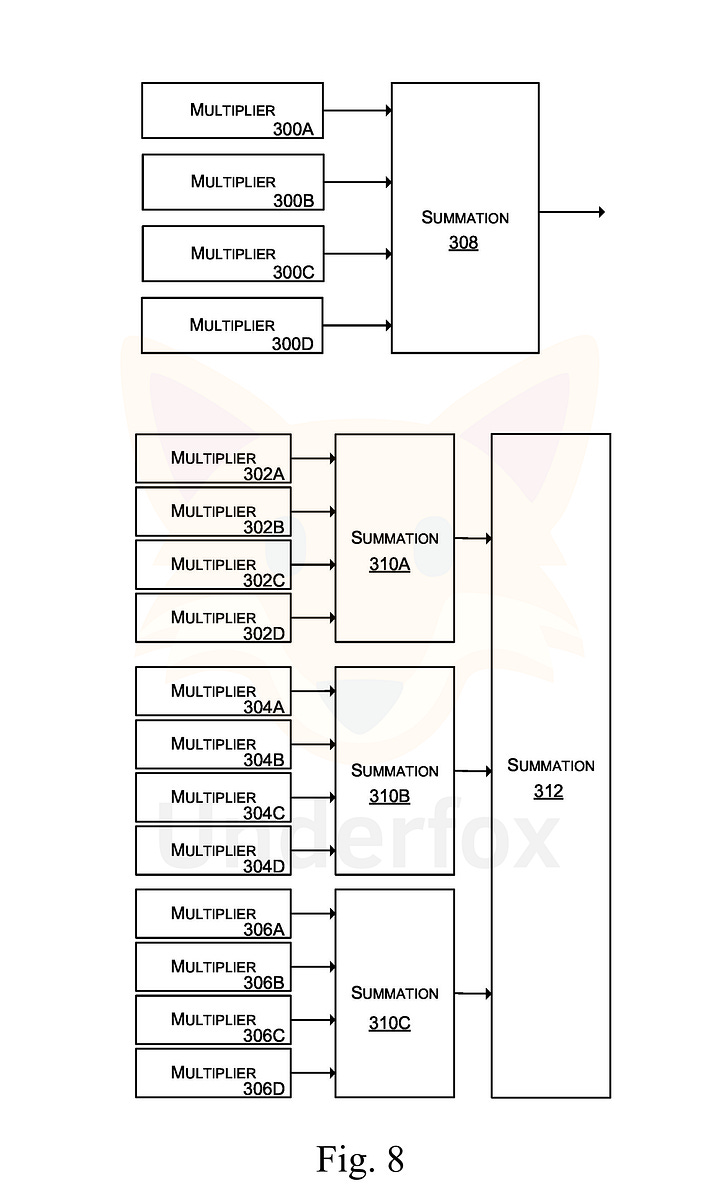

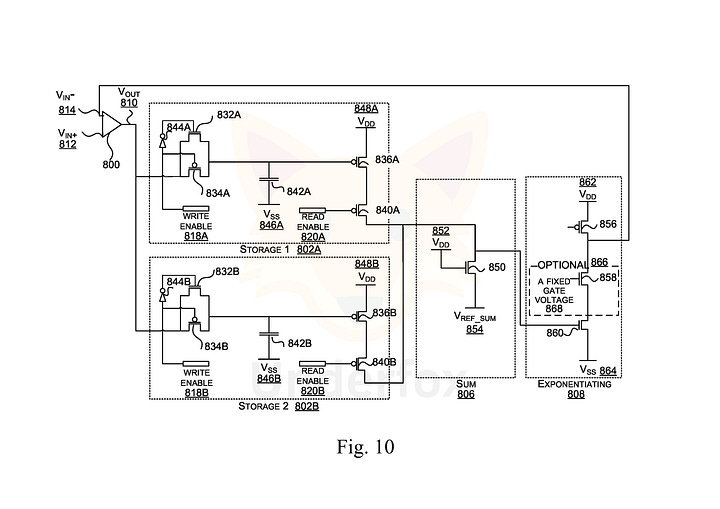
At this stage, it is important for the reader to understand that the duration of both the inference and training processes in end-to-end analog networks is determined by the equilibrium time of the circuit, which is on the order of nanoseconds, and is executed in analog by physics rather than simulated sequentially on a digital computer. Therefore, Fractile’s claim that its accelerator can achieve performance levels several orders of magnitude higher than the state of the art GPUs is entirely justified. Furthermore, a large part of the operations occurs at subthreshold voltages, making the accelerator vastly more efficient than modern GPUs.
The analog AI race is on!
At this point, it is essential to reflect on the development of analog electronics and machine learning over the last 30 years. Multiple incremental developments were also required to make this kind of analog AI accelerator feasible. In the last decade alone, there has been an unprecedented leap, culminating in the current race to develop the first commercial solution of this kind.
And why do I call this a race? Because Fractile is not the first to conceive this type of solution. For a few years now, Rain AI, another semiconductor startup aiming to compete with Nvidia, has been working on an AI accelerator based on the same principle as Fractile’s and has assembled a research team with some of the strongest names in the field. A key difference between the two approaches lies in the development of memristor IP. While Rain AI is focused on developing its own programmable resistor technology, there is no clear indication that Fractile will follow the exact same path. Therefore, Fractile may opt to leverage existing IPs already established in the industry, enabling faster product development. If, for example, Fractile reaches an agreement with GlobalFoundries and utilizes its 22FDX node and CBRAM technology, we could see a Fractile solution competing with Nvidia’s overpriced GPUs in a short timeframe.
With the potential to deliver a final product offering a significant performance advantage, exceptional energy efficiency, and a high-level library seamlessly integrated with PyTorch (the CUDA moat is an illusion), there is no doubt that Fractile could have a substantial chance of success. Indeed, we are on the verge of witnessing an unprecedented leap in the development of analog accelerators. And certainly such a race will take the current king of the hill out of his equilibrium point.
Some references and further reading:
WO2025012023 - Analog Multiplier Circuit - Stansfield et al. - Fractile [Link]
WO2024141751 - Analog Neural Network - Song et al. - Fractile [Link]
Benjamin Scellier, Yoshua Bengio, Equilibrium Propagation: Bridging the Gap Between Energy-Based Models and Backpropagation, Arxiv (2017) [Link]
Benjamin Scellier, Yoshua Bengio, Equivalence of Equilibrium Propagation and Recurrent Backpropagation, Arxiv (2018) [Link]
Benjamin Scellier, Anirudh Goyal, Jonathan Binas, Thomas Mesnard, Yoshua Bengio, Generalization of Equilibrium Propagation to Vector Field Dynamics, Arxiv (2018) [Link]
Changelog
v1.0 - Initial release;
Donations
Monero address: 83VkjZk6LEsTxMKGJyAPPaSLVEfHQcVuJQk65MSZ6WpJ5Adqc6zgDuBiHAnw4YdLaBHEX1P9Pn4SQ67bFhhrTykh1oFQwBQ
Ethereum address: 0x32ACeF70521C76f21A3A4dA3b396D34a232bC283